Introduction To Quadratic Equations And Inequalities

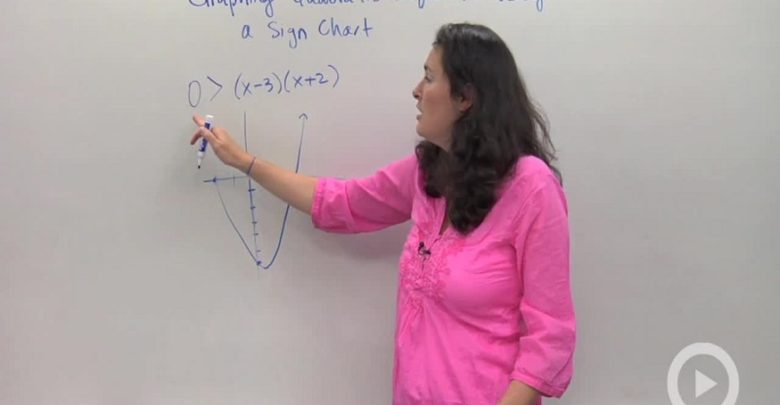
An equation of the form ax² + bx + c = 0 where x represents the unknown, a,b and c represents the known values and a ≠ 0. The numbers a,b and c are called the quadratic coefficients. The solution of the equation is the values which satisfy the given equation. A quadratic equation utmost has two solutions.

There are various methods to solve a quadratic equation namely:

• Factoring by inspection
• Completing the square

The general formula for solving a quadratic equation is

Here b² – 4ac is called the discriminant.

A quadratic equation consists of one or two distinct real roots, or distinct complex roots.

The discriminant determines the nature of the roots.

• The roots are distinct [both of which are real numbers] if the discriminant is positive.
• If there is exactly one real root called a double or repeated root, then the discriminant is zero.
• There are no real roots if the discriminant is negative. Rather there exist two distinct complex roots which are complex conjugates of one another.

Quadratic Inequalities

A mathematical statement which is identical to a quadratic equation but replaces the equal sign with inequality symbols such as greater than, lesser than is a quadratic inequality.

The quadratic inequalities are of the form ax² + bx + c = 0 where x represents the unknown, a,b and c represents the known values and a ≠ 0.

The following are the forms of quadratic inequalities:

• ax² + bx + c = 0 > 0
• ax² + bx + c = 0 ≥ 0
• ax² + bx + c = 0 < 0
• ax² + bx + c = 0 ≤ 0

There exist infinitely many solutions, one solution or no solution for a quadratic inequality.

Steps to solve a quadratic inequality are as follows:

• The inequality is written in the standard form with zero on the right-hand side.
• Determine whether the graph of the quadratic function lies above or below the x-axis. If the inequality consists of “less than”, then find the x-values below the x-axis and if it is “greater than”, then find the x-values above the x-axis.
• Quadratic inequalities are solved using a sign chart which indicates whether the function is above the x-axis using the positive signs or below the x-axis using the negative signs.
• Find the roots of the equation and make use of the sign chart to solve the quadratic inequality.